円すいの最短距離の練習問題
〔図Ⅰ〕のような直角三角形の1辺を軸とし、1回転させてときにできる立体について答えよ。
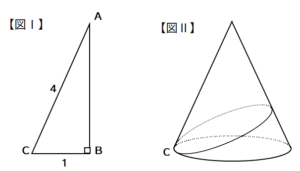
(1)辺ABを軸として1回転させたときの体積をV1とするとき、体積をV1を求めよ。
(2)(1)の立体について、〔図Ⅱ〕のように、点Cから側面を通って点Cまで1周する。そのときの最短距離を求めなさい。
(3)〔図Ⅰ〕の直角三角形を、辺BCを軸に1回転させたときの立体の体積をV2とする。このとき、V1:V2を求めよ。
円すいの最短距離の練習問題解答
(1)√15/3π
回転すると円すいができる。高さは、三平方の定理を利用して求める。
(2)4√2
円錐の最短距離の求め方➊まず展開図の中心角を求める
➋次に90°があれば、三平方の定理。そのほかの角度であれば、三平方の定理と相似などを組み合わせて解く
➋次に90°があれば、三平方の定理。そのほかの角度であれば、三平方の定理と相似などを組み合わせて解く
<例題>
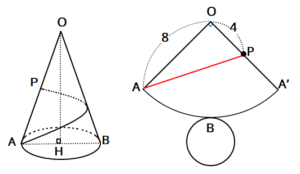
OA=8cm、AH=2cmである円錐がある。OAの中点に点PをとりAから側面上に回ってPまでいく最短距離を求めなさい。
<解法>
①おうぎ形の中心角=90°
②△AOPに注目して三平方の定理より、AP=4√5cmとなる。
(3)1:√15



コメント