中学2年生の数学で必ずテストに出るのが「平行四辺形の証明」です。
図形の性質を理由づけて説明する問題が多く、苦手に感じる人も多い単元ですが、頻出のパターンを押さえれば確実に得点できます。この記事では、平行四辺形になる条件や証明でよく使う定理、定期テストでよく出る問題を分かりやすくまとめました。証明の書き方に自信がない人も、ポイントを押さえてしっかり得点につなげましょう。
平行四辺形の証明の定期テスト対策予想問題
【問1】下図の平行四辺形ABCDで、対角線BD上に、2点E、FをBE=DFとなるようにとります。このとき、AE=CFであることを証明せよ
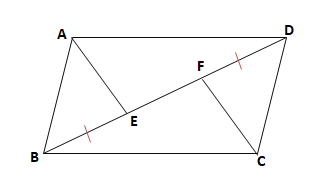
【問2】下の図のように、平行四辺形ABCDの辺CDの中点をEとし、辺ADの延長と線分BEの延長との交点をFとします。このとき、△EBC≡△EFDであることを証明せよ。
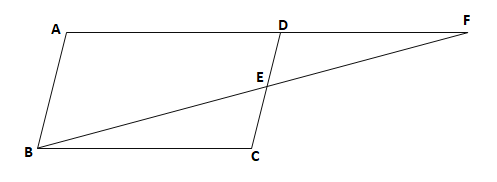
平行四辺形の証明の定期テスト対策予想問題の解答
【問1】
△ABEと△CDFで、
仮定より、BE=DF…①
平行四辺形の向かい合うは等しいので、AB=CD…②
AB//DCから、平行線の錯角は等しいので、∠ABE=∠CDF…③
①②③から、2組の辺とその間の角がそれぞれ等しいので、
△ABE=△CDF
合同な図形では、対応する辺は等しいので、 AE=CF
【問2】
△EBCと△EFDで
仮定より、EC=ED…①
対頂角は等しいから、∠BEC=∠FED…②
AF//BC から、平行線の錯角は等しいので、∠ECB=∠EDF…③
①②③から、1組の辺とその両端の角が、それぞれ等しいので、
△EBC=△EFD
平行四辺形の定義と性質
【定義】2組の向かいあう辺が、それぞれ平行な四角形です。
【性質】
- 平行四辺形の2組の向かいあう辺は、それぞれ等しい。
- 平行四辺形の2組の向かいあう角は、それぞれ等しい。
- 平行四辺形の対角線は、それぞれの中点で交わる。
平行四辺形の条件
- 2組の向かいあう辺が、それぞれ平行であるとき(定義)
- 2組の向かいあう辺が、それぞれ等しいとき
- 2組の向かいあう角が、それぞれ等しいとき
- 対角線が、それぞれの中点で交わるとき
- 1組の向かいあう辺が、等しく平行であるとき
平行四辺形の証明で使うポイント
平行四辺形の証明では、次のポイントを押さえると書きやすくなります。
- 平行線の性質:錯角や同位角を使って角の等しさを示す
- 三角形の合同条件:(辺・角・辺)、(角・辺・角)などを活用
- 対角線の中点:対角線の中点を利用して平行四辺形を判定
文章の順序:「理由 → 結論」の順で書くことを意識する。
定期テストでよく出る問題パターン
- 三角形の合同を使って平行四辺形であることを証明する
- 対角線の中点を利用して平行四辺形を判定する
- 一組の辺が平行かつ等しいことを示して平行四辺形とする


コメント