【中2数学】3学期学年末テスト対策予想問題

【中2数学】3学期学年末テスト対策予想問題です。中学2年生の3学期学年末テストでは、「図形の性質」「角度の求め方」「図形の証明」など、図形分野の総仕上げとなる単元が中心に出題されます。特に、合同条件や角度の性質を正しく使って証明を書く問題は、多くの生徒がつまずきやすいポイントです。この記事では、頻出問題の予想問題を掲載。得点源となる図形問題を効率よく対策し、学年末テストに備えましょう！

※テスト範囲が異なるときは、上記のリンクからそちらの問題を解いてください。

中2数学学年末テスト対策予想問題

問1　次の（　　　　）にあてはまることばを書きなさい。
（1）二等辺三角形の定義は、「（　　　）が等しい三角形」である。
（2）二等辺三角形の（　　　）の二等分線は（　　　）を垂直に2等分する。
（3）平行四辺形の定義は、「2組の（　　　）がそれぞれ平行な四角形」である。
（4）平行四辺形にの性質の1つは、「平行四辺形の（　　　　）は、それぞれの中点で交わる」である。
（5）長方形の定義は、「（　　　）がすべて等しい四角形」である。
（6）ひし形の対角線は、（　　　）という性質がある。
（7）長方形の辺について、「4つの辺がすべて等しい」という条件を加えると（　　　）になる。

問2　次のことがらの逆をいいなさい。またそれが正しいかどうかも答えよ。
（1）正三角形ならば、3つの角は等しい。
（2）△ABC≡△DEFならば、∠A＝∠D、∠B＝∠E、∠C＝∠Fである。
（3）a＞0、b＞0ならば、a+b＞0である。

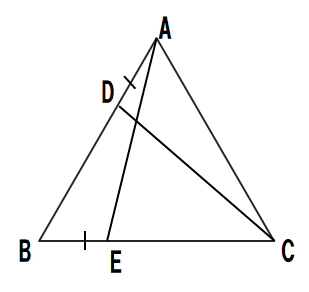
問3　正三角形ABCの辺AB、辺BC上に、点D,EをAD=BEとなるようによります。このとき、AE＝CDであることを証明せよ。

問4　四角形ABCDの対角線をOとするとき、次の条件のうちで、四角形ABCDがかならず平行四辺形になるもをすべて選び、記号で答えなさい。

ア　AB＝DC,AD＝BD
イ　AB＝DC、AD//BC
ウ　AB//DC,∠BAD＝∠DCB
エ　AB//DC、OB＝OD

問5　平行四辺形ABCDに次の条件が加わると、どんな四角形になるか答えよ、
（1）AB＝AD、∠A＝90°
（2）AC⊥BD

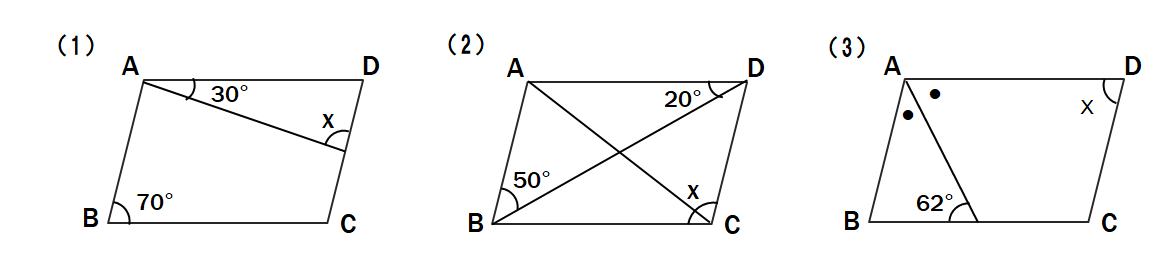
問6　次の図の平行四辺形ABCDで、同じ印をつけた辺や角は等しいとき、∠ｘの大きさを求めなさい。

問7　次の図で、四角形ABCDはAB＝5ｃｍ、BC=8ｃｍの平行四辺形である。∠ABCの二等分線と辺CDの延長が交わる点をEとします。このとき次の問いに答えなさい。

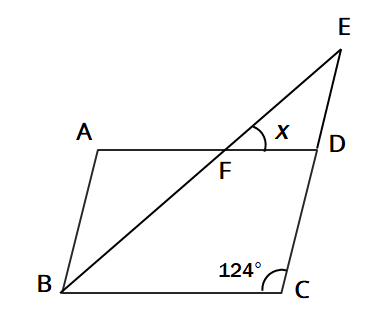
（1）∠ｘの大きさを求めなさい。
（2）線分DEの長さを求めよ。

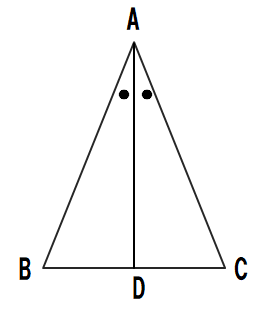
問8　定理「二等辺三角形の2つの底角は等しい」ということを次の図を利用して証明せよ。ただし、書き出しは、∠Aの二等分線をひき、辺BCとの交点をDとする。

問9　∠ｘの大きさを求めよ。ただし、同じ印をつけた角は等しい。

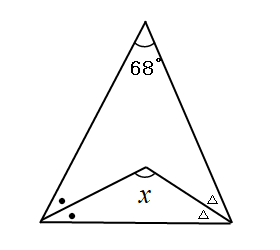
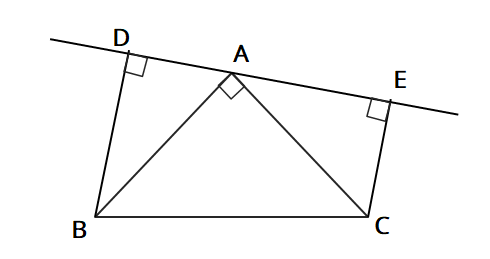
問10　図のように、∠A=90°の直角二等辺三角形ABCで、頂点Aを通る直線をひき、その直線に頂点B,Cから垂線BD,CEをひく。このとき、△BAD≡△ACDであることを証明せよ。

中2数学学年末テスト対策予想問題の解答

問1
（1）2つの辺
（2）頂角、底辺（完答）
（3）向かい合う辺
（4）対角線
（5）4つの角
（6）垂直に交わる
（7）正方形

問2
（1）3つの角が等しいならば、正三角形である。　（正しい）
（2）∠A＝∠D、∠B＝∠E、∠C＝∠Fならば、△ABC≡△DEFである。（正しくない）
（3）a+b＞0ならば、a＞0、b＞0である。（正しくない）

問3
△ABEと△CADにおいて
正三角形ABCより　AB＝CA…①
∠ABE＝∠CAD＝60°…②
仮定よりBE＝AD…③
①②③より、2組の辺とその間の角がそれぞれ等しいので、
△ABE≡△CAD
合同する図形の対応する辺は、等しいので、
AE＝CD

問4　ア、ウ、エ

問5
（1）正方形
（2）ひし形

問6
（1）80°
（2）110°
（3）56°

問7
（1）28°
（2）3ｃｍ

問8
∠Aの二等分線をひき、辺BCとの交点をDとする
△ABDと△ACDにおいて、
仮定より、AB＝AC…①
仮定より、∠BAD＝∠CAD…②
共通な辺より、AD＝AD…③
①②③より
2組の辺とその間の角がそれぞれ等しいので、
△ABD≡△ACD
合同な図形で対応する角は等しいので
∠ABD＝∠ACD
よって、二等辺三角形の2つの底角は等しい

問9
124°

問10
△BADと△ACEで、
仮定より、AB＝CA…①
AD⊥BD、∠AE⊥CEより、∠ADB＝∠CEA＝90°…②
三角形の内角の和は180°から
∠BAD＝180°ー90°ー∠BAD＝ 90°ー∠BAD …③
∠ACE＝180°ー90°ー∠BAD＝ 90°ー∠BAD …④
③④より、∠BAD=∠ACE…⑤
①②⑤より、
直角三角形の斜辺と1つの鋭角がそれぞれ等しいので、
△BAD≡△ACE
（随時更新）