【中学数学】確率の定期テスト対策予想問題です。
カードの確率の定期テスト対策予想問題
次の問いに答えなさい。
(1)箱の中に, 数字の1,2,3,3,4,4をそれぞ れ書いた6枚のカードが入っている。いま,この箱の中から同時に2枚のカードを取り出し,それぞれのカードに書かれている数の和を求めるとき,その和が偶数になる確率を求めよ。
(2)-2, -1, 0, 1,2の数が1つずつ書かれた5枚のカードがある。このカードをよくきってから1枚のカードをひき,そのカードをもとにもどし,よくきってから再び1枚のカードをひく。このとき, ひいた2 枚のカードに書かれた数の積が2以上になる確率を求めよ。
(3)数字2,3,4,5,6が書かれたカードがそれぞ れ1枚ずつある。この5枚のカードをよくきって, 1 枚ずつ2回続けて取り出す。1回目に取り出したカードに書かれた数を a, 2回目に取り出したカードに書 かれた数をbとするとき, a2-4b が2以上になる確 率を求めよ。ただし,取り出したカードはもとにもどさないものとする。
(4)袋Aの中には, 1から3までの数字を1つずつ記入した3枚のカード1, 2, 3が入っており,袋Bの中には, 4から7までの数字を1つずつ記入した4枚のカード4, 5, 6, 7が入っている。それぞれの袋の中のカードをよくかき混ぜてから,袋Aから1枚のカードを取り出し,そのカードに書かれている数をaとし,袋Bから1枚のカードを取り出し,そのカードに書かれている数をbとする。このとき,b>3aとなる確率を求めよ。
(5)数の書いてある5枚のカード[1], [2], [3] ,[4],[5]が箱に入っている。この箱から2枚のカードを同時に取 り出すとき, 取り出した2枚のカードに書いてある数の積が奇数である確率を求めよ。
(6)数字を書いた5枚のカード[1], [1], [2], [2], [3]がある。この5枚のカードをよくきって,その中から同時に2枚を取り出す。取り出した2枚のカードに書いてある数の和が4になる確率を求めよ。
(7)1,2,3,4,5の数字を1つずつ書いた5枚のカードがある。この5枚のカードから同時に3枚のカードを取り出すとき, 取り出した3枚のカードに書いてある数の和が偶数になる確率を求めよ。
(8)-1, 0,1の数を1つずつ書いた3枚のカードがある。このカードをよくきって1枚取り出し,書いてある数を読んでからもとにもどす。このことを3回行うとき, 取り出した3枚のカードに書いてある数の和が0となる確率を求めよ。
カードの確率の定期テスト対策予想問題の解答
(1)2/5
(2)6/25
(3)9/20
(4)5/12
(5)3/10
(6)3/10
(7)3/5
(8)7/27
さいころの確率の定期テスト対策予想問題
次の問いに答えなさい。
(1)2つのさいころを同時に投げるとき,出る目の数の和が素数である確率を求めよ。
(2)大小1つずつのさいころを同時に1回投げるとき、出る目の数の和が7以上になる確率を求めよ。
(3)A,B2つのさいころを同時に投げるとき、2つとも奇数の目が出る確率を求めよ。
(4)A,B2つのさいころを同時に投げるとき、出る目の数の和が5の倍数になる確率を求めよ。
(5)A,B2つのさいころを同時に投げるとき、Aの出る目の数がBの出る目の数の約数になる確率を求めよ。
(6)1つのさいころを1回投げるとき、偶数の目が出る確率を求めよ。
(7)1つのさいころをさいころを2回投げるとき、2回目に出る目の数が、1回目に出る目の数の倍数になる確率を求めよ。
(8)大小2つのさいころを同時に1回投げるとき、大小2つのさいころの出る目の数が同じになる確率を求めよ。
(9)大小2つのさいころを同時に、大小2つのさいころの出る目の数の和が4の倍数になる確率を求めよ。
(10)1から6までの目のついた2つのさいころA,Bを同時に1回投げる。このとき, Aのさいころの出る目の数が, Bのさいころの出る目の数よりも大きくなる 確率を求めよ。
さいころの確率の定期テスト対策予想問題の解答
(1)5/12
(2)7/12
(3)1/4
(4)7/36
(5)7/18
(6)1/2
(7)7/18
(8)1/6
(9)1/4
(10)5/12
コイン・硬貨の確率の定期テスト対策予想問題
次の問いに答えなさい
(1)3枚のコインがすべて表になる確率を求めなさい。
(2)2枚のコインがあります。これらのコインを同時に投げたとき、2枚とも表が出る確率を求めなさい。
(3)3枚のコインを同時に投げたとき、表が2枚と裏が1枚のパターンが出る確率を求めなさい。
(4)2枚の硬貨を同時に投げるとき、1枚が表で1枚が裏になる確率を求めなさい。
(5)3枚の硬貨を同時に投げるとき、1枚が表で2枚が裏になる確率を求めなさい。
(6)10円硬貨、50円硬貨、100円硬貨を同時に3枚投げるとき、表が出た硬貨の合計が100円以上となる確率を求めなさい。
(7)3枚の硬貨を同時に投げるとき、少なくとも1枚が表になる確率を求めなさい。
(8)4枚の硬貨を同時に投げるとき、4枚とも表になる確率を求めよ。
(9)4枚の硬貨を同時に投げるとき、少なくとも1枚が表になる確率を求めなさい。
(10)1つのサイコロと1枚の硬貨を同時に投げるとき,硬貨が表の場合はサイコロの出た目の数を2倍し,裏の場合はサイコロの出た目の数を2乗した。このとき計算した値が9以下となる確率を求めなさい。
コイン・硬貨の確率の定期テスト対策予想問題の解答
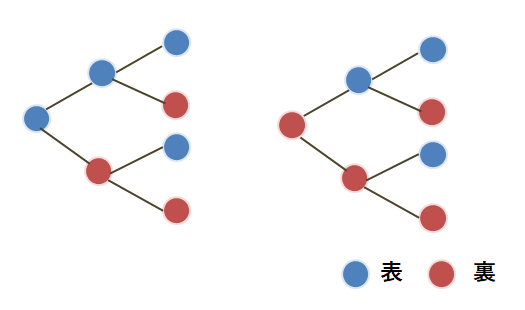
コイン・硬貨の樹形図
つまり、コインを3枚投げたときのパターンは、(表表表)、(表表裏)、(表裏表)、(表裏裏)、(裏表表)、(裏表裏)、(裏裏表)、(裏裏裏)の8通りとなります。
(1)1/8
(2)1/4
(3)3/8
(4)1/2
(5)3/8
(6)3/8
(7)7/8
(8)1/16
(9)15/16
(10)7/12


コメント