中学2年生の数学で登場する「直角三角形の合同の証明」は、入試や定期テストでも頻出の重要単元です。特に応用問題では、条件の見抜き方や証明の組み立て方がポイントになります。このページでは、直角三角形の合同の条件（斜辺と1つの鋭角／斜辺と他の1辺）を復習しつつ、応用問題でよく出るパターンとその解き方のコツをわかりやすく解説します。図形の論理的思考を鍛えて、証明問題を得意分野に変えましょう！
直角三角形の合同の証明（応用問題）
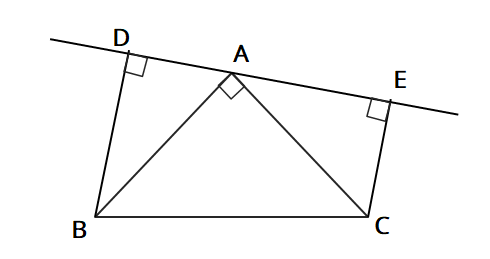
図のように、∠A=90°の直角二等辺三角形ABCで、頂点Aを通る直線をひき、その直線に頂点B,Cから垂線BD,CEをひく。このとき、△BAD≡△ACDであることを証明せよ。
直角三角形の合同の証明（応用問題）解答
△BADと△ACEで、
仮定より、AB＝CA…①
AD⊥BD、∠AE⊥CEより、∠ADB＝∠CEA＝90°…②
三角形の内角の和は180°から
∠BAD＝180°ー90°ー∠BAD＝ 90°ー∠BAD …③
∠ACE＝180°ー90°ー∠BAD＝ 90°ー∠BAD …④
③④より、∠BAD=∠ACE…⑤
①②⑤より、
直角三角形の斜辺と1つの鋭角がそれぞれ等しいので、
△BAD≡△ACE
直角三角形の合同の証明｜よく出るパターンとコツまとめ
直角三角形では、以下の2つの合同条件
- 斜辺と1つの鋭角がそれぞれ等しい →「斜辺と1つの鋭角がそれぞれ等しい ⇒ 合同」
- 斜辺と他の1辺がそれぞれ等しい →「斜辺と他の1辺がそれぞれ等しい ⇒ 合同」
証明でよく出るパターン
- 共通な辺を使って「1辺が等しい」とする問題
- 直角三角形で「斜辺」が与えられているパターン
- 補助線（垂線など）を引くことで直角三角形ができる問題
- 二等辺三角形や角の二等分線を利用する問題
証明のコツ
図をしっかり見る！
→「共通な辺」や「直角」など、合同の条件に使えそうな情報を探す。
証明の型を覚える！
→「○○と△△において、〜より、合同条件○○で、合同がいえる。」という流れを意識。
条件を見逃さない！
→「直角三角形」と書かれていたら、合同条件の中でも特別な2つを使えるチャンス！
図に書き込む！
→ 等しい辺・角には記号（「／」「✔︎」など）を書いて整理するとミスが減る。
コメント