高校入試の数学で毎年のように出題される「図形分野」は、苦手にしやすい単元ですが、パターンをおさえれば得点源になります。角度、面積、相似、円周角、三平方の定理など、よく出る問題パターンを中心に予想問題を厳選し、詳しい解答・解説付きでわかりやすくまとめました。入試本番で慌てないためにも、今のうちにしっかり対策しておきましょう!
数学の図形の予想問題(公立高校入試)
【平面図形編1】
線分ABを直径とする円Oがある。下の図のように、円周上に点Cをとる。点Cから線分AB上に垂線をひき、その交点をDとする。また、∠CABの二等分線と線分BC、線分CDとの交点をそれぞれ、点F、点Eとし、点Fから線分ABに垂線をひき、その交点をGとする
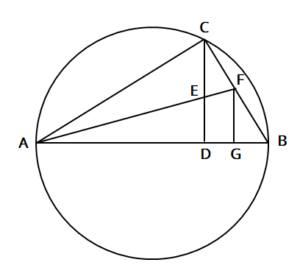
(1)CF=GFになることを証明せよ。
(2)AB=5cm、AC=4cmのとき、CDの長さを求めなさい。
【空間図形編1】
図1は、頂点をO,底面の円の中心をH,直径A,Bとする円すいである。また、図2は、図1の円すいに外から接する正三角錐O-XYZである。円すいの底面の円の半径が3、体積が18πのとき、次の問いに答えなさい。
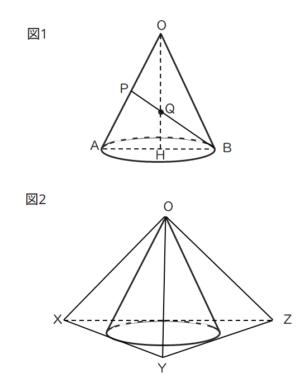
(1)母線OAの長さを求めなさい。
(2)円すいの表面積を求めなさい。
(3)図1のように、母線OAの中点をPとし、線分PBとOHとの交点をQとする。PQの長さを求めなさい。
(4)正三角錐O-XYZの体積を求めなさい。
【平面図形の問題2】
図のように円Oの外の点Aから円Oに2本の接線を引き、その接点をそれぞれB,Cとします。線分OAと円の交点をDとします。またOB=8cm、∠AOB=60°とし、線分ABと線分ACのそれぞれに接する半径2の円Pがあります。次の問いに答えなさい。
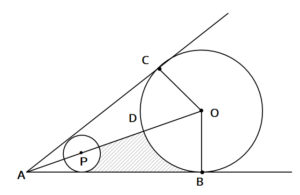
(1)点Cを含まない弧BDの長さを求めなさい。
(2)線分OPの長さを求めなさい。
(3)斜線部分の面積を求めなさい。
【空間図形の問題2】
図のように、OA=OB=OC=2、OA⊥OB、OB⊥OC、∠AOC=120°の三角すいOABCがある。また、BD:DA=BE:EC=1:2となる点D、EをそれぞれAB、BC上にとる。
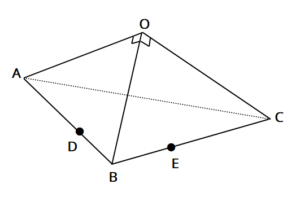
(1)DEの長さを求めなさい。
(2)三角すいOABCの体積を求めなさい。
(3)三角すいODBEの体積を求めなさい。
数学の図形の予想問題(公立高校入試)の解答
【平面図形編1】
(1)△ACFと△AGFにおいて
AF=AF(共通)…①
∠CAF=∠GAF(仮定)…②
∠ACF=∠AGF=90°…③
①②③より、直角三角形で斜辺と1つの鋭角がそれぞれ等しいので
△ACF≡△AGF 対応する辺は等しいから、CF=GFとなる。
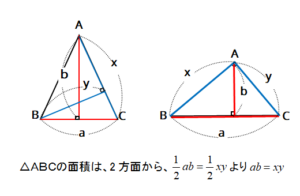
(2)直角三角形ABCを2方面からとらえる
△ABCに着目して、特別な直角三角形(3:4:5)より、BC=3cmとなる。
下の公式より、AC×CB=AB=CDとなるので、
4×3=5×CDを解くことになり、CD= 12/5となる。
【空間図形編1】
(1)3√5
(2)9π+9√5π
(3)√13/2
(4)54√3
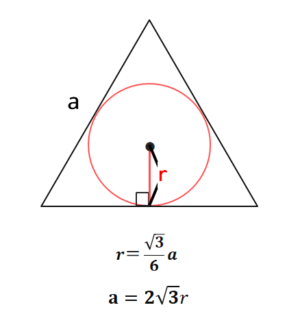
正三角形の内接円の半径の関係を利用する
【平面図形の問題2】
(1)8/3π
(2)12
(3)30√3ー12π
【空間図形の問題2】
(1)2√3/3
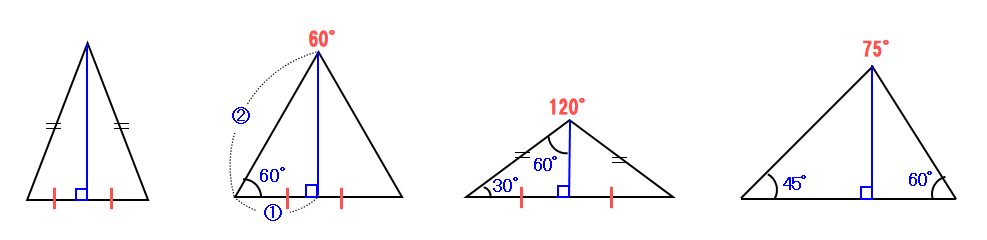
線分ABは、△OCAに着目して、点Oから線分ACに垂線を下ろし交点をHとすると、△AOHは、特別な直角三角形(1:2:√3 )となり、AO:AH=
2:√3=2:AHなので、AH=√3。AC=2AHなので、AC=2√3。
△BDE∽△BCA(2角相等より)なので、BD:BA=DE:ACから、1:3=DE:2√3 DE=2√3/3となる。
(2)2√3/3
(3)2√3/27
△ABC:△DBE=3:1の相似なので、面積は、9:1となる。
よって、三角すいOABC:三角すいODBEの体積=△ABC:△DBE=9:1


コメント