メネラウスの定理を使った練習問題
図のようにAB=6cm,AC=4cmの△ABCで、∠Aの二等分線と辺BCとの交点をDとし、BAの延長とCを通りADに平行な直線の交点をEとする。また、CからADに垂線をひき、AD,ABとの交点をそれぞれH,Iとする。このとき次の問いに答えなさい。
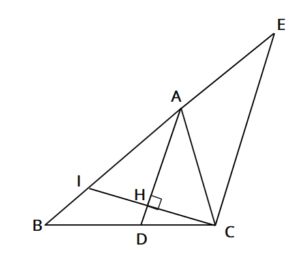
(1)BD:DCを求めよ。
(2)AI:IBを求めよ。
(3)AH:HDを求めよ。
メネラウスの定理を使った練習問題の解答
(1)3:2
角の二等分線定理を利用して解きます。
(2)2:1
△AHCは二等辺三角形であることを見抜くことがポイント
(3)5:1
メネラウスの定理を利用して解くといいでしょう。
メネラウスの定理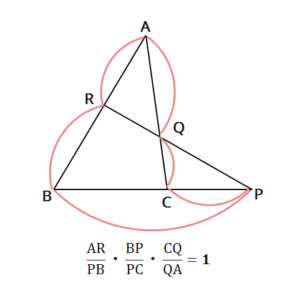




コメント