【中3数学】折り返し図形×相似の融合問題を攻略！高校入試頻出のコツを解説

高校入試数学でよく出題される「折り返し図形」と「相似」の融合問題。見た目が複雑で一見難しそうに感じますが、ポイントを押さえれば解きやすくなります。本記事では、出題傾向や頻出パターンを踏まえながら、折り返し図形と相似の基本から応用までをわかりやすく解説します。入試本番で差がつくこの単元を、しっかりと得点源に変えていきましょう！

折り返し図形と相似の融合問題

下の図のような1辺の長さが30ｃｍの正三角形ＯＡＢにおいて、辺ＯＡ上に点Ｃ、辺ＯＢ上に点Ｄをとる。線分ＣＤを折り目として△ＯＣＤを折り返すと、頂点Ｏは辺ＡＢ上の点Ｅと重なる。ＯＣ＝21ｃｍ、ＢＥ＝6ｃｍのとき、次の問いに答えよ。

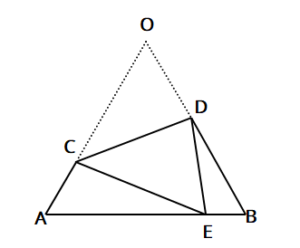
（1）△ＡＥＣ∽△ＢＤＥであることを証明せよ。

（2）線分ＤＥの長さを求めよ。

折り返し図形と相似の融合問題解説

（1）△ＡＥＣと△ＢＤＥにおいて
∠ＣＡＥ＝∠ＥＢＤ＝60°…①　　
∠ＡＥＣ＝180°-（∠ＢＥＤ+∠ＤＥＣ）…②
∠ＢＤＥ＝180°-（∠ＢＥＤ+∠ＤＢＥ）…③　
ここで、∠ＤＥＣ＝∠ＤＢＥ＝60°なので
②③より、2組の角がそれぞれ等しい。　
よって、△ＡＥＣ∽△ＢＤＥ

（2）14ｃｍ

（1）より、△ＡＥＣ∽△ＢＤＥなので、図示より

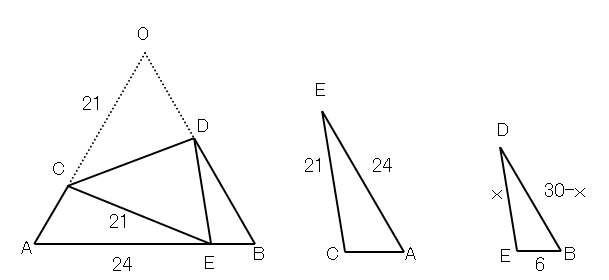
ＣＥ：ＥＤ＝ＥＡ：ＤＢなので、21：ｘ＝24：（30-ｘ）　これを解くと、ｘ＝14となる。