【中3数学】2学期中間テスト対策予想問題

【中3数学】2学期中間テスト対策予想問題です。主な単元は、小問集合（中1～中3のこれまでの履修内容）、平方根、二次方程式、二次関数がメインとなっています。

2学期中間テスト対策予想問題（中3数学）

【問1】次の問いに答えなさい。
（1）100の平方根を答えなさい。

（2）二次方程式ax²+bx+c=0の解答の公式を答えよ。

（3）xとｙの関係が（　　　）＜aは定数＞で表すとき、yはxの2乗に比例するという。（　　）にあてはまる式を答えなさい。

（4）関数y=2x²のグラフは、（　　　）を対称の軸として（　　　）である。（　　）にあてはまる語句をそれぞれ答えなさい。

（5）a=5,b=-4のとき、-3a+b²の値はを求めなさい。

（6）等式a+2b=17をbについて解きなさい。

（7）一次方程式9x+13=2(x-4)を解きなさい。

（8）連立方程式
x-2y=4
4x+3y=5を解きなさい。

（9）yはxに反比例し、x=4のとき、y=-6である。x=-3のときのyの値を求めなさい。

（10）5本のうち1本のあたりくじが入っているくじがある。このくじを同時に2本をひくとき、あたりくじがふくまれる確率を求めなさい。

【問2】次の方程式を解きなさい。
（1）x²=16

（2）-5x²＝-40

（3）(x-1)²=7

（4）x²=7x

（5）x²-6x-16=0

（6）x²+3x-28=0

（7）2x+35=x²

（8）4x²-9x+2=0

（9）（x－1）（x-5）=2

【問3】次の各問に答えなさい。
（1）x=√6+2、y=√6-2のときx²-y²の値を求めなさい。

（2）√10の整数部分をa、小数部分をbとするとき、a+b(b+6)の値を求めなさい。

（3）次の数の中から最も大きい数を選び、ア～エの記号で答えなさい。

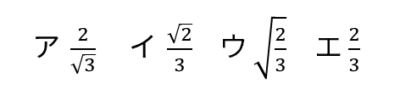
（4）√19-3nの整数となるような正の整数nの値をすべて求めなさい。

（5）二次方程式x²-6x+a=0の解の1つが2であるとき、もう1つの解を求めなさい。

（6）二次方程式x(x-a)+12=0の2つの解がともに正の整数になるとき、aの値をすべて求めなさい。

【問4】次の問いに答えなさい。
(1) xについての2次方程式x²-8x+a=0の解の1つがx=3のとき,aの値を求めなさい。また,もう1つの解を求めなさい。
(2) xについての2次方程式x²+ax-8=0の解の1つがx=8のとき,aの値を求めなさい。また,もう1つの解を求めなさい。
(3) xについての2次方程式x²+ax+b=0の解がx=1, 7のとき,a, bの値を求めなさい。
(4) xについての2次方程式x²+ax+b=0の解がx=-2, -4のとき,a, bの値を求めなさい。

【問5】次の問いに答えなさい。
（1）2つの自然数があり、2数の差は7である。この2数の積が78のとき、大きい方の数を求めなさい。

（2）連続する3つの自然数がある。最大の数の2乗は、他の数をそれぞれ2乗したものの和に等しい。この3つの自然数を求めなさい。

（3）横が縦より5cm長い長方形の厚紙があります。この厚紙の4すみから、1辺3cmの正方形を切り取って、ふたのない箱をつくったところ、その容積が108cm³になりました。もとの厚紙の縦の長さを求めなさい。

（4）横が縦より5cm長い長方形の紙があります。この紙の4すみから1辺が4cmの正方形を切り取り、直方体の容器をつくったところ、容積144cm³になりました。もとの長方形の縦の長さを求めなさい。

（5）幅16cmの鉄板を左右同じ長さだけ折り曲げ、切り口の長方形の面積を30cm²にします。鉄板を左右何cmずつ折り曲げればよいですか。

（6）差が5で、積が84になる2つの正の数を求めよ。

【問6】次のア～オの関数について、あとの問いに記号で答えなさい。

（1）グラフが上に開いているものはどれか。
（2）グラフがx軸について対称であるものはどれとどれか。
（3）グラフの開き方がもっとも小さいものはどれですか。

【問7】図のようなAB=BC=12cmの直角三角形ABCで、点PはAを出発して辺AB上をBまで動く。また、点Qは、点PがAを出発するのと同時にＢを出発し、点Pと同じ速さで辺BC上をCまで動く。

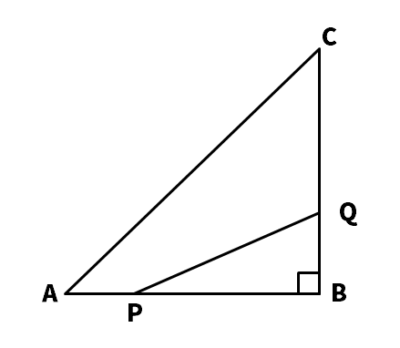
（1）点PがAからxcm動いたとき、PB,BQの長さをxを使って表しなさい。
（2）点PがAから何cm動いたとき、△PBQの面積が16cm²になるか求めなさい。

【問8】次の図は、関数y=-x+6のグラフで、このグラフとx軸との交点をAとする。点Pは、x軸上を原点OからAまで毎秒1cmの速さで動く。点Qは関数y=-x+6のグラフ上の点で、つねに、線分PQがy軸に平行になるように動く。△QPAの面積が8のとき、点Qの座標を求めなさい。

2学期中間テスト対策予想問題（中3数学）の解答

【問1】
（1）±10
（2）x=-b±√b2-4ac/2a
（3）y=ax2
（4）y軸、線対称
（5）1
（6）b=(17-a)/2
（7）x=-3
（8）x=2,y=-1
（9）8
（10）2/5

【問2】
（1）x=±4
（2）x=±2√2
（3）x=1±√7
（4）x=0,7
（5）x=-2,8
（6）x=-7,4
（7）x=-5,7
（8）x=2,1/4
（9）x=3±√6

【問3】
（1）8√6
（2）a=3 b=√10-3
（3）ア
（4）1,5,6
（5）4
（6）a=7,8,13

【問4】
(1)a=15 もう1つの解x=5
(2)a=-7 もう1つの解x=-1
(3)a=8,b=7
(4)a=6,b=8

【問5】
（1）13
（2）3，4，5

（3）縦の長さをｘcmとすると、横の長さは(ｘ+5)cm である。4すみから3cmずつ切り取るので、箱の縦横はそれぞれ6cm短くなる。

3(x-60)(x-1)=108
(x-6)(x-1)=36
x²-7x-30 = 0
(x+3)(x-10)=0
よって、x=-3, 10
x>6であるから、x=10は問題にあっているが、
x=-3はあわない。
よって、x=10

（4）縦の長さをxcmとすると、横の長さは(x+5)cm である。4すみから4cmずつ切り取るので、箱の高さは4cm、縦は(x-8)cm、横x+5-8=(x-3)cm となる。
4(x-8)(x-3)=144
(x-8)(x-3)=36
x²-11x-12=0
(x+1)(x-12)=0
x+1=0, x-12=0
よって、x=-1, 12
x>8であるから、
x=12 は問題にあっているが、
x=-1はあわない。
よって、x=12

（5）縦の長さをxcmとすると、横の長さは(16-2x)cm になる。
x(16-2x)=30
16x-2x²=30
x²-8x-15=0
(x-3)(x-5)=0
よって、
x=3,5
0<x<8であるから、これらは問題にあっている。

（6）小さい方の数をxとすると、大きい方の数はx+5だから、方程式は、x(x+3)=84
これを解くと、x=7, -12。
xは正の数だから、x=7。
大きい方の数は、7+5=12
7と12

【問6】
（1）ア、ウ
（2）ウとエ
（3）イ

【問7】
（1）PB=12-x BQ=x
（2）4cm，8cm

【問8】
Q（2，4）