連比の練習問題
図のように、平行四辺形ABCDがある。辺ABを中点をEとし、点Eを通り線分BDに平行な直線と辺ADとの交点をFとする。また、線分CFと線分ED,BDとの交点をそれぞれG,Hとする。このとき、次の問いに答えなさい。
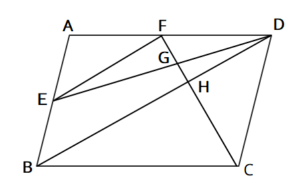
(1)△AEF∽△ABDであることを証明しなさい。
(2)△FHDの面積は、台形ABCFの面積の何倍か求めなさい。
(3)CH:HGを最も簡単な整数の比で表しなさい。
連比の練習問題の解答
(1)△AEFと△ABDにおいて
共通な角より、∠EAF=∠BAD…①
EF//BDより ∠AEF=∠ABD…②
①②より2組の角がそれぞれ等しいので
△AEF∽△ABD
(2)1:9
面積比の公式を利用する
面積比の公式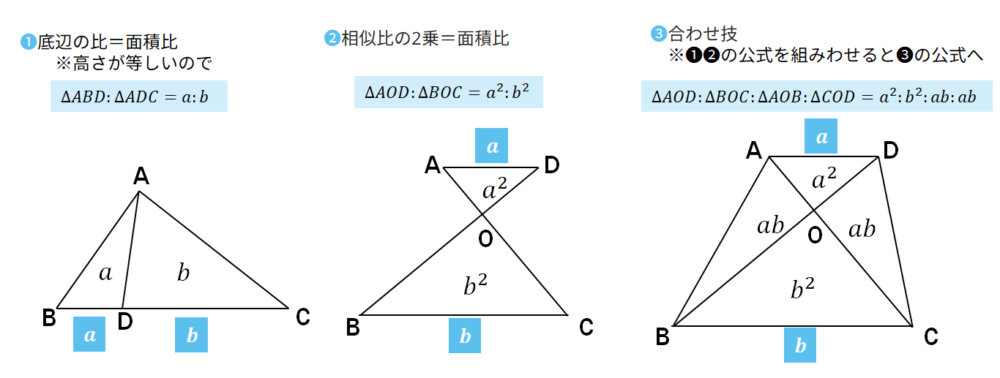

(3)5:1
比合わせ(連比)の公式。最小公倍数で合わせることがポイント
比合わせ(連比)の公式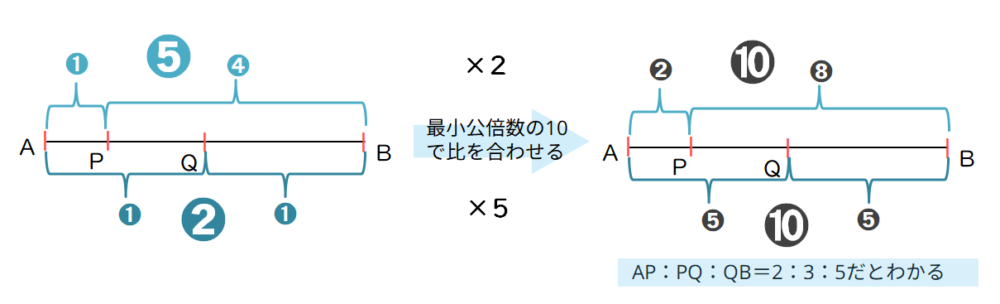



コメント