空間図形と三平方の定理の練習問題
図のように、すべての辺の長さが6の正四角錐O-ABCDがあり、辺AB,BCの中点をそれぞれM,Nとして△OMNをつくる。次の問いに答えなさい。
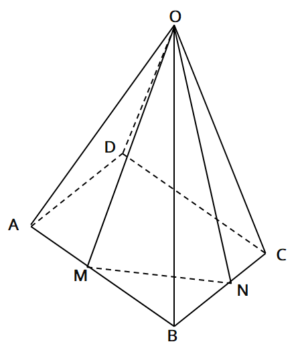
(1)辺MNの長さを求めなさい。
(2)△OMNの面積を求めなさい。
(3)正四角錐O-ABCDの体積を求めなさい。
(4)頂点Bから平面OMNに下ろした垂線の長さを求めなさい。
空間図形と三平方の定理の練習問題の解答
(1)3√2
正方形ABCDの対角線ACを引き、中点連結定理より3√2
(2)9√5/2
△OMNは二等辺三角形。高さは三平方の定理で求める。
(3)36
高さは三平方の定理で求める。
(4)3√5/5
B-OMNの体積=O-BMNの体積に着目して方程式を利用して解く。(同じ体積を2方面から求めていることの利用)
2方面シリーズ(空間図形編)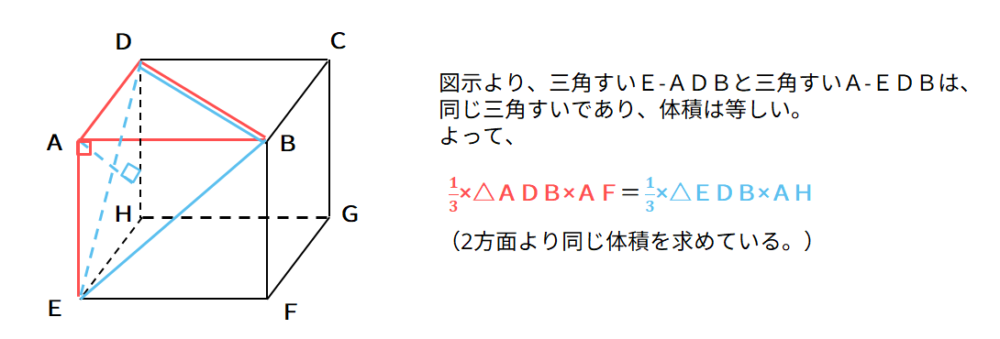



コメント