外接円の半径に関する練習問題
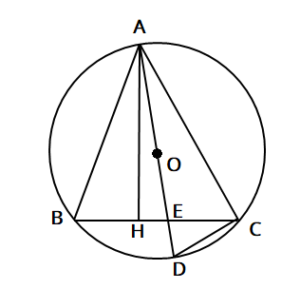
△ABCの3つの頂点は円Oの周上にあり、AB=√5cm、BC=3cm、CA=2√2cmである。また、点Dも円Oの周上にあり、ADは直径となる。さらに、点Aから辺BCへ垂線をひき、その交点をHとし、ADとBCの交点をEとする。
(1)△ABH∽△ADCになることを証明せよ。
(2)BH=xとする、CH=3-xとなる。△ABHと△ACHで三平方の定理を利用してBHの長さを求めなさい。
(3)円Oの半径を求めなさい。
外接円の半径に関する練習問題の解答
(1)△ABHと△ADCで
∠AHB=90°(仮定) ∠ACD=90°(半円を弧とする円周角)
よって、∠AHB=∠ACD…① ∠ABH=∠ADC(弧ACの円周角)…②
①②より、2組の角がそれぞれ等しいので△ABH∽△ADC
(2)1
AH2=AB2ーBH2=AC2ーCH2
BH=xとすると
AH2=( √5)2ーx2=(2√2 )2ー(3ーx)2
これを解くと、x=1となる。
BH=xとすると
AH2=( √5)2ーx2=(2√2 )2ー(3ーx)2
これを解くと、x=1となる。
(3)√10/2
AHの長さは、△ABHに着目すると、三平方の定理より、
AH2=AB2 -BH2なのでAH2=( √5)2 -12これを
解くと、AH=2となる。
よって、△ABCの面積は、 1/2×3×2=3
求める円Oの半径は、外接円の半径の求め方より√10/2
AH2=AB2 -BH2なのでAH2=( √5)2 -12これを
解くと、AH=2となる。
よって、△ABCの面積は、 1/2×3×2=3
求める円Oの半径は、外接円の半径の求め方より√10/2
外接円の半径の求め方



コメント