【高校入試対策】数学の図形の発展問題（偏差値65突破の問題）

【高校入試対策】数学の図形の発展問題（偏差値65突破の問題）です。

数学の図形の発展問題

【平面図形の問題】
図のように円Oの外の点Aから円Oに2本の接線を引き、その接点をそれぞれB,Cとします。線分OAと円の交点をDとします。またOB＝8ｃｍ、∠AOB＝60°とし、線分ABと線分ACのそれぞれに接する半径2の円Pがあります。次の問いに答えなさい。

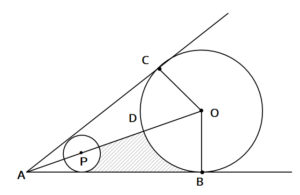
（1）点Cを含まない弧BDの長さを求めなさい。
（2）線分OPの長さを求めなさい。
（3）斜線部分の面積を求めなさい。

【空間図形の問題】
図のように、OA＝OB＝OC＝2、OA⊥OB、OB⊥OC、∠AOC＝120°の三角すいOABCがある。また、BD：DA＝BE：EC＝1：2となる点D、EをそれぞれAB、BC上にとる。

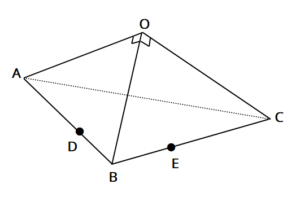
（1）DEの長さを求めなさい。
（2）三角すいOABCの体積を求めなさい。
（3）三角すいODBEの体積を求めなさい。

【平面図形の問題】
（1）8/3π

おうぎ形の弧の長さ＝直径×（中心角/360）　

（2）12　

特別な直角三角形よりＡＯの16ｃｍ。Ｐから線分ＡＢに垂線をひき交点をＨ。△ＡＰＨ∽△ＡＯＢを地ようする。

（3）30√3ー12π

台形ＰＨＢＯ－（Ｐを含むおうぎ形+Ｏを含むおうぎ形）

【空間図形の問題】
（1）2√3/3

まず、線分ＡＣを求め、△ＢＤＥ∽△ＢＣＡの帽子型で線分ＤＥを導くのがポイント。

線分ＡＢは、△ＯＣＡに着目して、点Ｏから線分ＡＣに垂線を下ろし交点をＨとすると、△ＡＯＨは、特別な直角三角形（1：2：√3 ）となり、ＡＯ：ＡＨ＝

2：√3＝2：ＡＨなので、ＡＨ＝√3。ＡＣ＝2ＡＨなので、ＡＣ＝2√3。

△ＢＤＥ∽△ＢＣＡ（2角相等より）なので、ＢＤ：ＢＡ＝ＤＥ：ＡＣから、1：3＝ＤＥ：2√3 　ＤＥ＝2√3/3となる。

垂線を下す決め手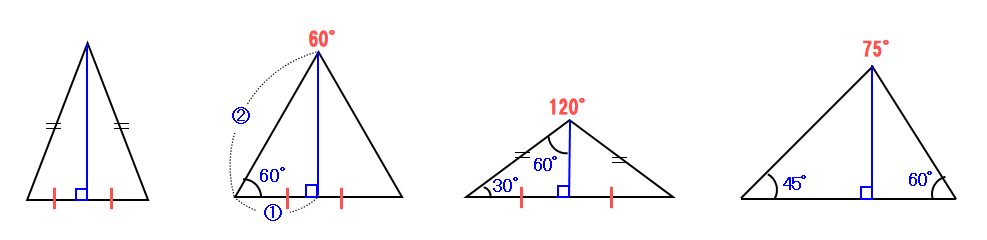

（2）2√3/3

三角すいOABCの体積は、底面を△AOCにすると、高さは、線分OBとなる。

（3）2√3/27

高さが共通しているので、三角すいOABC：三角すいODBEの体積＝△ＡＢＣ：△ＤＢＥ
△ＡＢＣ：△ＤＢＥ＝3：1の相似なので、面積は、9：1となる。
よって、三角すいOABC：三角すいODBEの体積＝△ＡＢＣ：△ＤＢＥ＝9：1