【高校入試対策数学】折り返し図形と三平方の定理の問題

折り返し図形と三平方の定理の問題

図において、四角形ABCDは縦18ｃｍ、横30ｃｍの長方形である。PD＝PQ、PAは∠DPQの二等分線であるとき、次の問いに答えよ。

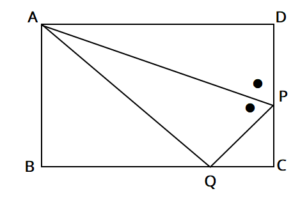
（1）AQの長さを求めよ。

（2）PQの長さを求めよ。

（3）APの長さを求めよ。

（1）30

△ＡＱＰ≡△ＡＤＰ（二辺とその間の角がそれぞれ等しい）より、ＡＱ＝ＡＤ＝30となる。

折り返し図形（折り返した頂点が対辺上にあるとき）

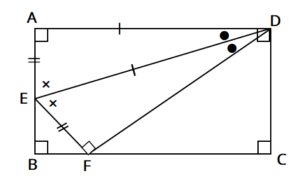
必ず

合同な図形　△ＡＥＤ≡△ＦＥＤ
相似な図形　△ＥＢＦ∽△ＦＣＤ　ができる。

【合同である証明】
△ＡＥＤと△ＦＥＤにおいて
ＤＥ＝ＤＥ（共通）…①
ＡＥ＝ＦＥ（仮定）…②
∠ＡＣＥ＝∠ＦＤＥ…③
2辺とその間の角がそれぞれ等しいので、△ＡＥＤ≡△ＦＥＤ

相似である証明】
△ＥＢＦと△ＦＣＤにおいて
∠ＥＢＦ＝∠ＦＣＤ＝90°…①
∠ＥＦＢ＝90°-∠ＤＦＣ…②　∠ＦＣＤ＝90°-∠ＤＦＣ…③
②③より、∠ＥＦＢ＝∠ＦＣＤ…④　①④より、2組の角がそれぞれ等しい。
よって、△ＥＢＦ∽△ＦＣＤ

（2）10

ＰＱ＝ｘとすると、ＱＰ＝（18-ｘ）となる。
またＢＱは、△ＡＱＢに着目して、三平方の定理を利用し、ＢＱ²＝ＡＱ²-ＡＢ²より、ＢＱ＝24となる。
ここで、△ＡＱＢ∽△ＱＰＣなので、ＡＱ：ＱＰ＝ＢＱ：ＣＰより、30：ｘ＝（18-ｘ）：24　これを解くとｘ＝10となる。

（3）10√10

（2）より、ＰＱ＝10より、ＰＤ＝10となる。ＡＰは、△ＡＤＰに着目し、三平方の定理より、ＡＰ²＝ＡＤ²+ＰＤ²となり