「円周角の定理」は中学数学の図形分野の中でも、定期テストに高確率で出題される重要な単元です。角度の関係を見抜く力や図形の特徴を正しく読み取る力が問われます。この記事では、円周角の定理の基本から応用まで、テストに出やすい問題を厳選し、わかりやすい解説付きで紹介します。テスト対策や直前の総復習にぜひ活用してください!
■ 円周角の角度を求めるポイント
- 共通する弧の円周角と中心角の関係は、円周角:中心角=1:2
- 共通する弧の円周角を等しい
- 弧の比と円周角の比は等しい(弧の長さは円周角に比例する)
- 内接する四角形の定理
以上の4点を必ず押さえておく。そのうえで、これまで履修してきた三角形の外角の定理、対頂角は等しいなどの性質を頭の片隅に置きながら解いていく。
円周角の定理の定期テスト対策予想問題
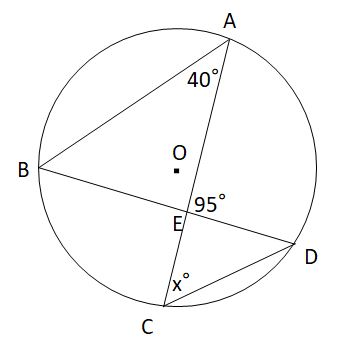
(1)図のように、円Oの円周上に4点A,B,C,Dがある。∠BAE=40°,∠AED=95°のとき、Xの値(∠ECD)を求めよ。
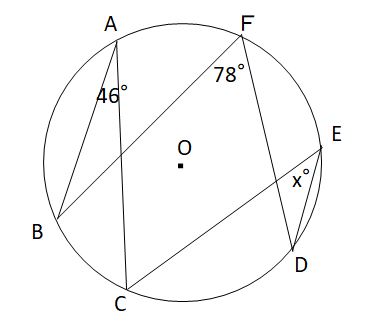
(2)図のように、円Oの円周上に6点A,B,C,D,E,Fがある。∠BAC=46°,∠BFD=78°のとき、Xの値(∠CED)を求めよ。
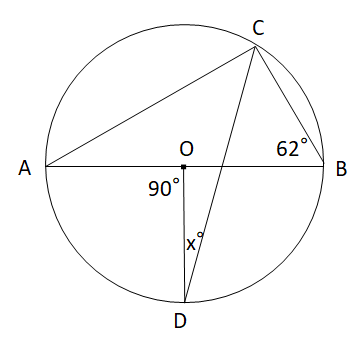
(3)図のように、円Oの円周上に4点A,B,C,Dがある。∠CBA=62°,∠AOD=90°のとき、Xの値(∠CDO)を求めよ。
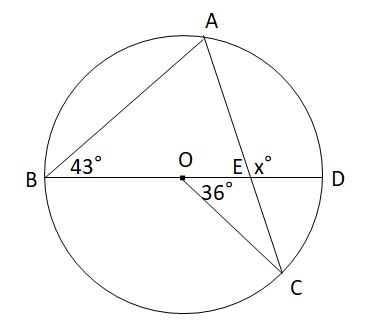
(4)図のように、円Oの円周上に4点A,B,C,Dがある。∠CAB=62°,∠AOD=90°のとき、Xの値(∠AED)を求めよ。
円周角の定理の定期テスト対策予想問題の解答
- 55°
- 32°
- 17°
- 115°
円周角の定理 解き方のコツまとめ
1. 円周角の定理とは?
- 弧に対する中心角は、円周角の2倍になる。
- 同じ弧に対する円周角はすべて等しい。
- 弧をはさんでできる円周角は180度(=半円に対する円周角は直角)。
2. 解き方のコツ
① 図の中にある弧に注目する!
→ 弧に対してどの点から角ができているかを確認
→ 「同じ弧を見てる角は同じ角度だな」と気づくのが第一歩!
② 角度の関係を線でなぞる
→ 弧や角の両端を線で結んでみると、円周角の関係が見えてくる!
→ 補助線を引くのも有効!
③ 中心角との関係も活用する
→ 中心角がわかっていれば円周角はその半分!
④ 半円(直径)を見つけたら「直角」を疑え!
→ 半円に対する円周角は必ず90度!
→ 三角形が直角三角形になっている可能性も!


コメント