【中1理科】力のはたらきの要点まとめ｜重力・摩擦・圧力・ばねの力をわかりやすく解説！

中学1年理科で学ぶ「力のはたらき」は、今後の物理分野の土台になるとても大切な単元です。重力・摩擦力・圧力・ばねの力など、私たちの身の回りで働いているさまざまな力の性質と特徴を理解することがポイントです。
この記事では、それぞれの力の特徴や公式、グラフの読み取り方まで、定期テストや入試で問われやすい内容をわかりやすくまとめています。暗記だけでなく「なぜそうなるのか？」を理解しながら、得点につながる力を身につけましょう！

身のまわりの力の種類

• 重力…地球が物体を地球の中心に向かって引く力。すべての物体にはたらく
• 弾性力…ばねやゴムなどが変形したときに、元の形に戻ろうとする力
• 抗力（垂直抗力）…机や床などが物体を支える力。面に垂直にはたらく
• 摩擦力…物体同士がこすれ合うときに生じる、動きを妨げる力
• 磁力…磁石が鉄などの物体を引きつけたり、反発したりする力
• 張力…ひもや糸が物体を引っ張るときにはたらく力

力のはたらき

力のはたらきは、（１）物体の形を変える、（２）物体持ち上げる。また、支える。（３）物体の向きを変える。と3つあります。

いろいろな力

• 弾性力（弾性の力）…弾性（変形した物体が元に戻ろうとする性質）によって生じた力。机の上に物体があるときも、机を物体にはたらく重力でわずかに変形し、弾性力が生じます。
• 摩擦力（摩擦の力）…ふれ合っている物体の間で、物体のはたらきをさまたげるようにはたらく力。
• 磁力（磁石の力）…磁石と鉄などの物質、磁石と磁石の間にはたらく力。
• 電気の力…物体どうしをこすり合わせたときに生じる電気によってはたらく力。
• 重力…地球がその中心に向かって物体を引く力。地球上のすべての物体にはたらいている。

力の大きさ

力の大きさは、ばねに加わる力の大きさが変わるとばねののびも変わるので、ばねではかることができる。単位は、ニュートン。（記号Ｎ）。 1Ｎの力は約100gの物体にはたらく重力と同じ大きさ。

• フックの法則…ばねやゴムのような弾性をもつ物体の変形の大きさが、加えた力に比例する関係。ばねののびは、ばねにはたらく力の大きさに比例します。ばねなど、弾性のある物体の変形の大きさは加えた力の大きさに比例する関係のこと。

力の表し方

力の3つの要素として、大きさ、向き、作用点（物体に力がはたらく点）の3つがあります。力を表す矢印は、作用点から、力のの向きに、力の大きさに比例した長さの比で矢印を書いて表します。

• 作用線…力の矢印をふくむ線

重さと質量のちがい

• 重さ…物体にはたらく重力のことで、場所によって変わります。ばねばかりではかり、単位はＮを使います。
• 質量…物体の分量のことで、場所が変わっても、変化しません。上皿てんびんではかります。単位は、Kg、gを使用。

地球上と月面において、質量は変わりませんが、重さは月面では、地球の1/6となります。月面の重力は、地球の重力の1/6だからです。

力の大きさとばねののび

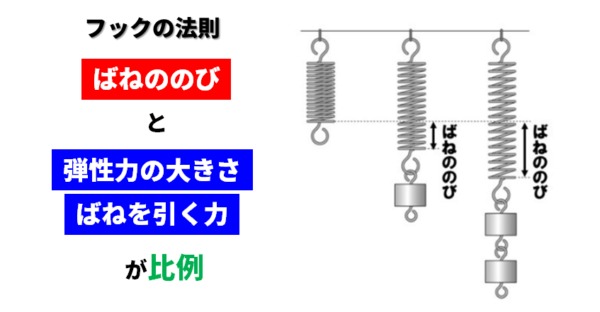
フックの法則は、「ばねを引く力の大きさとばねののびは比例する」という法則です。

ばねを引く力の大きさをF、ばねの自然長からののびをXとすると、
フックの法則は、F=kx (f:ばねを引くカの大きさ、x:ばねののび、k:比例定数) と表せる。

弾性定数（ばね定数）

等式変形（式を変形すると）、k＝F/xとなり、これは、「弾性定数」または「ばね定数」とよばれる量である。

式からわかるように、kは「単位長さだけばねをのばすのに必要な力の大きさ」を表している。

したがってkの値の大きなばねは、のばすのに大きな力を要することになので、「のばしにくいばね」、あるいは、「かたいばね」ということになります。

Kの単位は、N/mやkg重/mなどである。このようなばねの性質を利用して力の大きさを調べる道具に、ばねばかりがある。

ばねのグラフ
力の大きさとばねののびの関係を調べる。

＜手順＞

1. ばねに分銅をつり下げ、のびを読みとります。
2. 分銅をふやして、同じように読みとります。

＜結果＞

分銅の質量（g）	0	20	40	60	80	100
力の大きさ（N）	0	0.2	0.4	0.6	0.8	1
ばねののび（ｃｍ）	0	0.9	2.0	3.1	4.1	5.0

グラフを書くと原点を通る直線になります。つまり比例します。

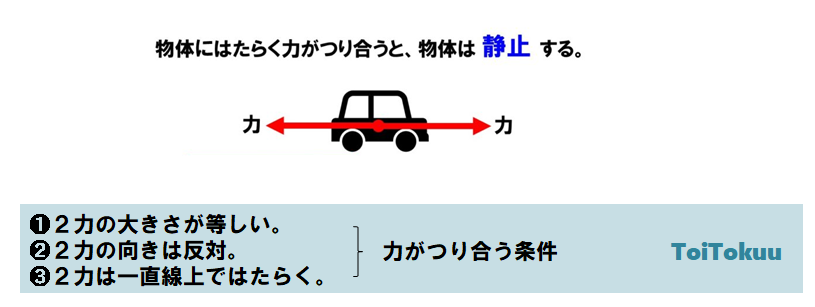
力のつり合い

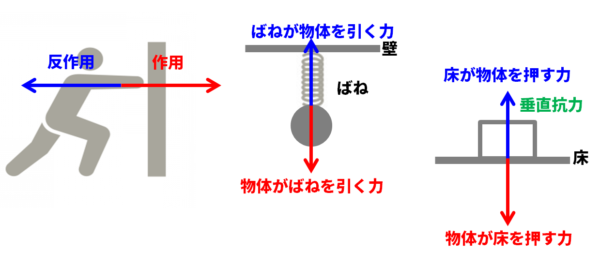
物体Aが物体Bに力を加えるときには、物体Aは物体Bから必ず力を受けます。このとき、物体Aが物体Bに加える力を作用、物体Bが物体Aにおよぼす力を反作用といいます。

• 作用と反作用の大きさは等しく、同一直線上にあり、向きが反対です。

ばねの一端を固定し、もういっぽうの端を手で引っ 張ってみると、手を引いた向きとは反対の向きにばねが手を引っ張っている。また、ブランコにのった人が、隣のブランコにのった人を引っ張ると、自分も相手のほうに引き寄せられる。このとき、一方の力を作用といい、他方の力を反作用という。

作用と反作用の法則

作用と反作用の法則は、同じ直線上ではたらき、大きさが等しく、向きが反対で、それぞれ別の物体にはたらいている法則。ニュートンの運動の第三法則ともいう。2つの物体の間で、一方が他方に力をはたらかせるとき、必ず相手からも自分のほうに対して力がはたらいていることから生じます。

• 大きさが等しい
• 向きが反対
• （作用点が同じ）※重力などは例外

作用・反作用の例

作用・反作用の関係にある2力を見つけるポイントは、作用点を見ることです。力がはたらく点である作用点が同じだからです。その作用点からそれぞれ別の物体に逆向きにはたらいている力を見つければいいのです。

例えば、物体が床に置いてある場合のことを考えてみてください。

• 物体が床を押す
• 床も物体を押し返す