【中1数学】1学期期末テスト対策予想問題です。中学1年生にとって最初の大きな関門ともいえる1学期期末テスト。特に数学では、「正負の数」「文字式」「方程式」など、初めて学ぶ内容が盛りだくさんです。この記事では、これまでの出題傾向をもとに厳選した予想問題を、解答・解説付きで紹介しています。テスト前の総仕上げや、苦手単元の克服に役立つ内容となっているので、ぜひ活用してください。
【問題】1学期期末テスト対策予想問題（中1数学）
【問1】次の（1）～（4）の（ ）にあてはまる言葉、数を答えなさい。
（1）正の数でも負の数でもない数は、（ ）です。
（2）a,b,cがどんな数であっても、(a×b)×c=a×(b×c)が成り立ちます。この法則を「乗法の（ ）」といいます。
（3）同じ数をいくつかかけ合わせてものを、その数の（ ）といいます。
（4）2つの数の積が+1があるとき、一方の数を他方の数の（ ）といいます。
【問2】次の（1）～（3）の問いに答えなさい。
（1）次の式の項を、すべていいなさい。
-2+3-4
（2）「自然数から自然数を引いた差は、自然数である。」
この文章は正しいですか。正しければ○、正しくなければ×を書きなさい。
（3）次の数を左側から小さい数に並べなさい。
-23 , (-3)2 , -32
【問3】次の（1）～（10）の計算をしなさい。
【問4】次の表は、Aさん、Bさん、Cさん、Dさんの4人がバスケットボールの試合で決めた得点を示したものです。次の問いに答えなさい。
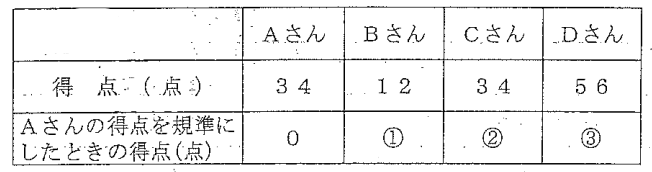
（1）Aさんの得点を基準とすると、Bさん、Cさん、Dさんの得点は、どのように表せますか。表の➀～➂にあてはまる数を書きなさい。
（2）（1）の結果をもとに、4人の平均得点を求めなさい。
【問5】次の（1）～（4）の式を、式を書くときの約束にしたがって表しなさい。
（1）3×x+y×4
（2）z×(-0.1)×z-z×2
（3）a÷5-b÷6
（4）7×c÷8
【問6】ある商品を買って、1000円札を出したときのおつりについて考えた。次の問いに答えなさい。
（1）商品の代金が800円のとき、おつりを求める式を書きなさい。
（2）商品の代金がa円のとき、おつりを表す式を書きなさい。
【問7】次の式を、文字式を書くときのきまりにしたがって表しなさい。
（1）a×4
（2）b× (-5)×a
（3）x×x×x
（4）(x+y)×(x+y)×a×(-1)
【問8】次の計算をしなさい。
➊2ｘ＋3－5ｘ－6
➋3ｘ－（4ｘ－2）
➌－3ｘ×2
➍2（3ｘ－5）
【問9】次のことがらが成り立つことを文字式を使って説明しなさい。
（1）連続する2つの奇数の和は4の倍数である。
（2）連続する3つの偶数の和は6の倍数である。
【問10】十の位の数字と一の位の数字の和が9である2けたの整数は9の倍数である。このことがらが成り立つことを文字式を使って説明しなさい。
【問11】「連続する3つの整数の和は3の倍数である」ことを説明しなさい。
【問12】連続する2つの整数の和は奇数であることの説明しなさい。
【解答】1学期期末テスト対策予想問題（中1数学）
【問1】
（1）0
（2）結合法則
（3）累乗
（4）逆数
【問2】
（1）-2,+3,-4
（2）☓
（3）-32 , -23 , (-3)2
【問3】
（1）-12
（2）-6
（3）360
（4）-1/8
（5）-128
（6）-8
（7）3/2
（8）-4
（9）16
（10）1
【問4】
（1）➀-22 ➁0 ➂+22
（2）34点
【問5】
（1）3x+4y
（2）-0.1z2-2z
（3）a/5-b/6
（4）7c/8
積（かけ算の答え）と商（割り算の答え）のルール（決まり）をまとめています。
積の表し方
- 文字式では、乗法の記号×をはぶいて書く。[例] axb=ab, 3×z=3z
- 文字と数の積では,数を文字の前に書く。[例] xx2=2x, yx (-5) = -5y
- 文字と文字の積では、ふつうアルファベット順に書く。[例] bXcXa=abc
- 1や-1と文字との積では, 1をはぶいて書く。[例] 1Xx=x, yx (-1)=-y (注) 0.1, 0.01, …などと文字の積では, 1をはぶくことはできない。0.1×a=0.1a であり, 0.a とするのは誤り。
- 同じ文字の積は、累乗の指数を使って書く。
商の表し方
- 除法の記号は使わず、分数の形で書く。
四則の混じった式の表し方
- X, ÷は使わずに書くが, +やーは,はぶけない。
【問6】
（1）1000-800円
（2）1000-a
文字を使用して、式を表します。これまでことばや○, 口などで表していた数や量を文字(アルファベット)を使って表す。
数量を表す文字の入っている式
[例] 1本50円の鉛筆x本の代金を表す式は、50×x(円)＝(1本の値段)×(本数)
文字式は、ことがらを一般的に表すことができる。
【問7】
（1）4a
（2）-5ab
（3）x3
（4）-a(x+y)2
- 積は、乗法の記号×をはぶいて書く。
- 数は文字の前に書く。
- 文字はふつうアルファベット順に書く。
- かっこに入った式は1つの文字と考える。また, -1 との積では1をはぶく。
【問8】
➊2ｘ＋3－5ｘ－6
＝2ｘ－5ｘ＋3－6
＝－3ｘ－3
➋3ｘ－（4ｘ－2）
＝3ｘ－4ｘ＋2
＝－ｘ＋2
➌－3ｘ×2
＝－6ｘ
➍2（3ｘ－5）
＝6ｘ－10
➊文字と数があるときは、文字どうし、数どうしの項を、まとめることができます。
➋（ ）があるときは、外して計算します。ー（ ）は減法のときのように、（ ）の中の符号は変わります。
➌文字式と数字の掛け算と割り算は、係数をどうしを計算します。
➍項が2つ以上の式は、分配法則の要領で計算します。
【問9】
（1）連続する2つの奇数は、nを整数として、2n-1,2n+1 と表すことができる。
その和は (2n-1)+(2n+1) =4nで、
nは整数だから、4nは4の倍数である。
（2）連続する3つの偶数は、nを整数として、2n-2,2n,2n+2と表すことができる。
その和は(2n-2) + 2n + (2n+2) = 6nで、
nは整数だから、6nは6の倍数である。
あることがらが成り立つことを、文字式を使って一般的に説明できることがある。
整数の表し方
整数についてのことがらを説明するときによく使われる。
nを整数として
- 偶数…2n
- 奇数…2n-1(または 2n+1)
- 3の倍数…3m
- 3でわると1余る数…3n+1
- 連続する3つの整数…n-1, n, n+1
【問10】
nを1けたの自然数とし、十の位をnとすると一の位の数は9-nと表されるから、
2けたの整数は、10n + (9-n) = 9n +9=9(n+1)
n+1は整数だから、9(n+1)は9の倍数である。
【問11】
nを整数として、連続する3つの整数を n-1, n, n+1 と表すことができる。
このとき、3つの整数の和は、(n-1) + n+(n+1) = 3n
nは整数だから3nは、3の倍数であるので、連続する3つの整数の和は3の倍数である。
【問12】
連続する2つの整数は、 nを整数としてn, n+1 と表すことができる。
このときこれらの2つの整数の和は、 n+(n+1)=2n+1
2n+1 は奇数を表すから、
連続する2つの整数の和は奇数である。
コメント