三角形の合同の証明応用問題
△ABCで、辺AB、辺ACをそれぞれ1辺とする正三角形△ABD、△ACEを、△ABCの外側につくります。このとき、BE=DCであることを証明しなさい。
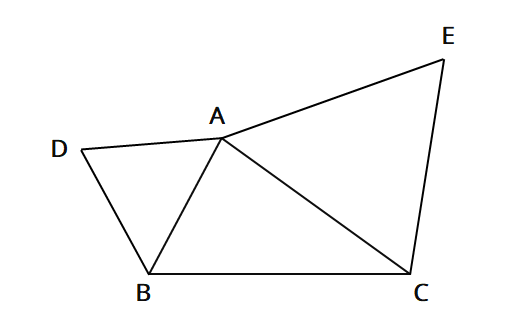
三角形の合同の証明応用問題の解答
△ABEと△ADCにおいて
△ABDは正三角形なので、AB=AD…①
△ACEは正三角形なので、AE=AC…①
正三角形の1つの内角は60°だから
∠EAB=60°+∠BAC…③
∠CAD=60°+∠BAC…④
③④より、∠EAB=∠CAD…⑤
∠EAB=60°+∠BAC…③
∠CAD=60°+∠BAC…④
③④より、∠EAB=∠CAD…⑤
①②⑤より
2組の辺とその間の角がそれぞれ等しいので、
△ABE≡△ADC
合同な図形では、対応する辺hの長さは等しいので
BE=DC


コメント